COVID-19 AI and Simulation Project

Research Results：RQ3_2021

Simulation of infection spread and control

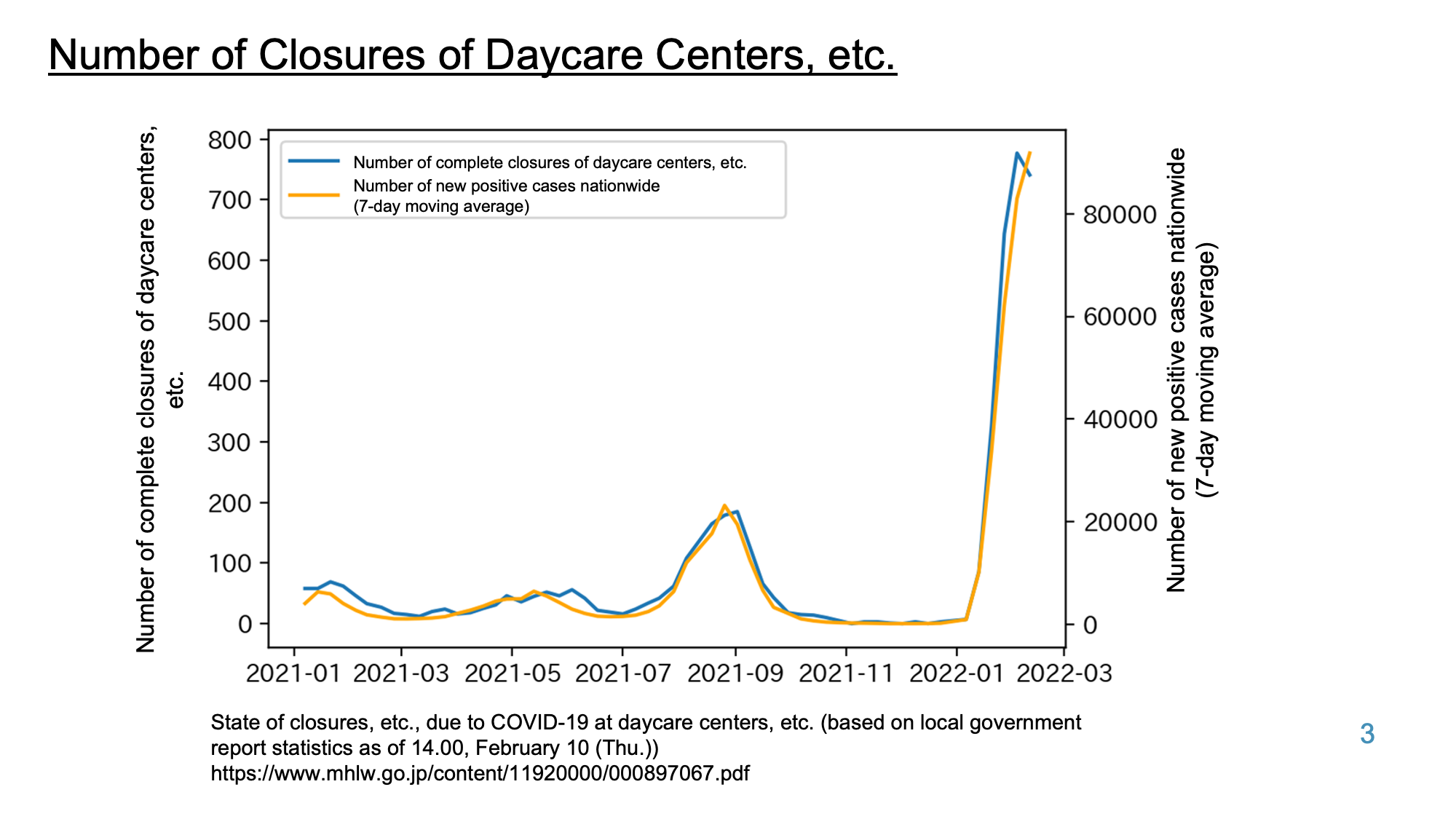
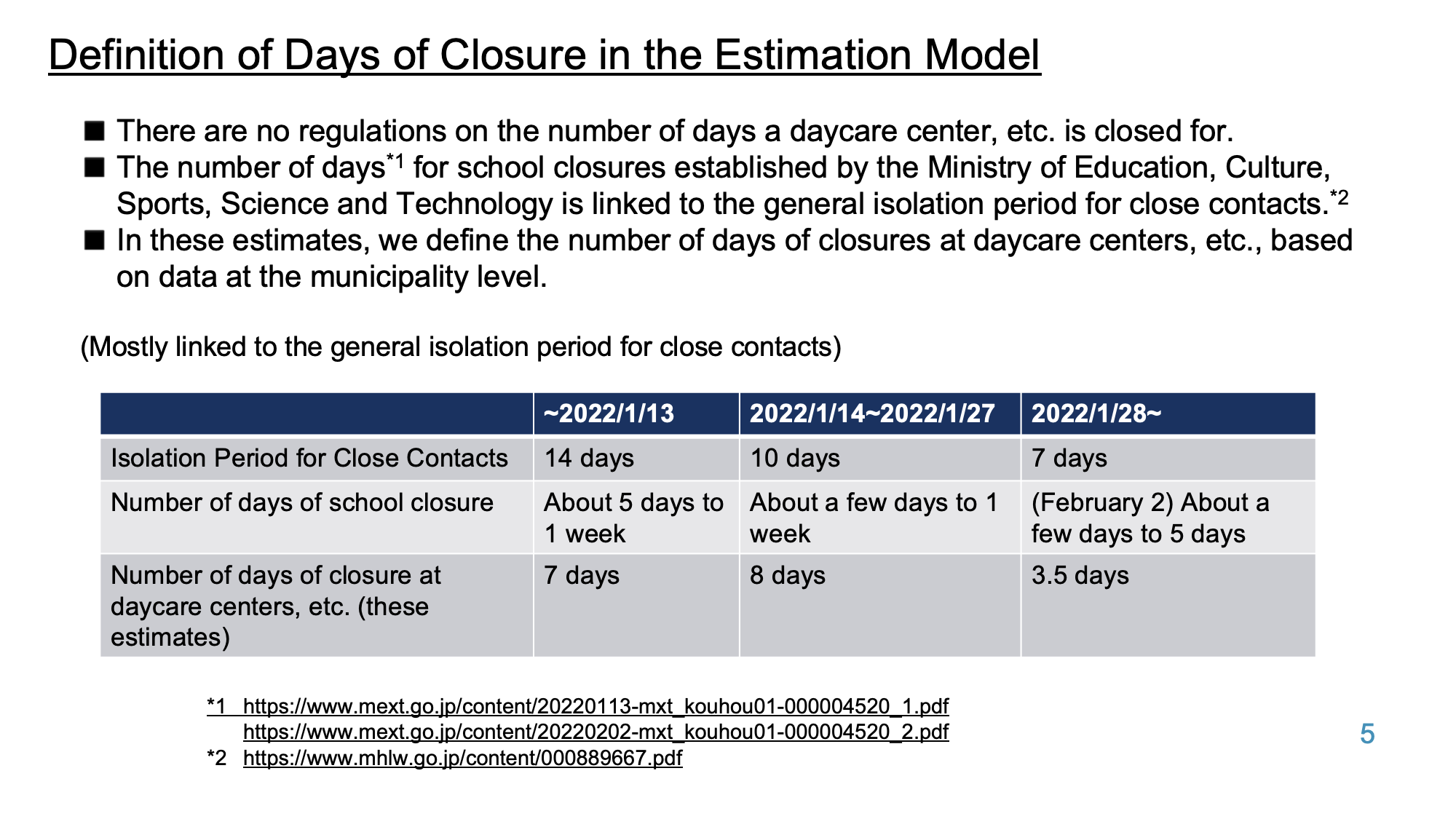
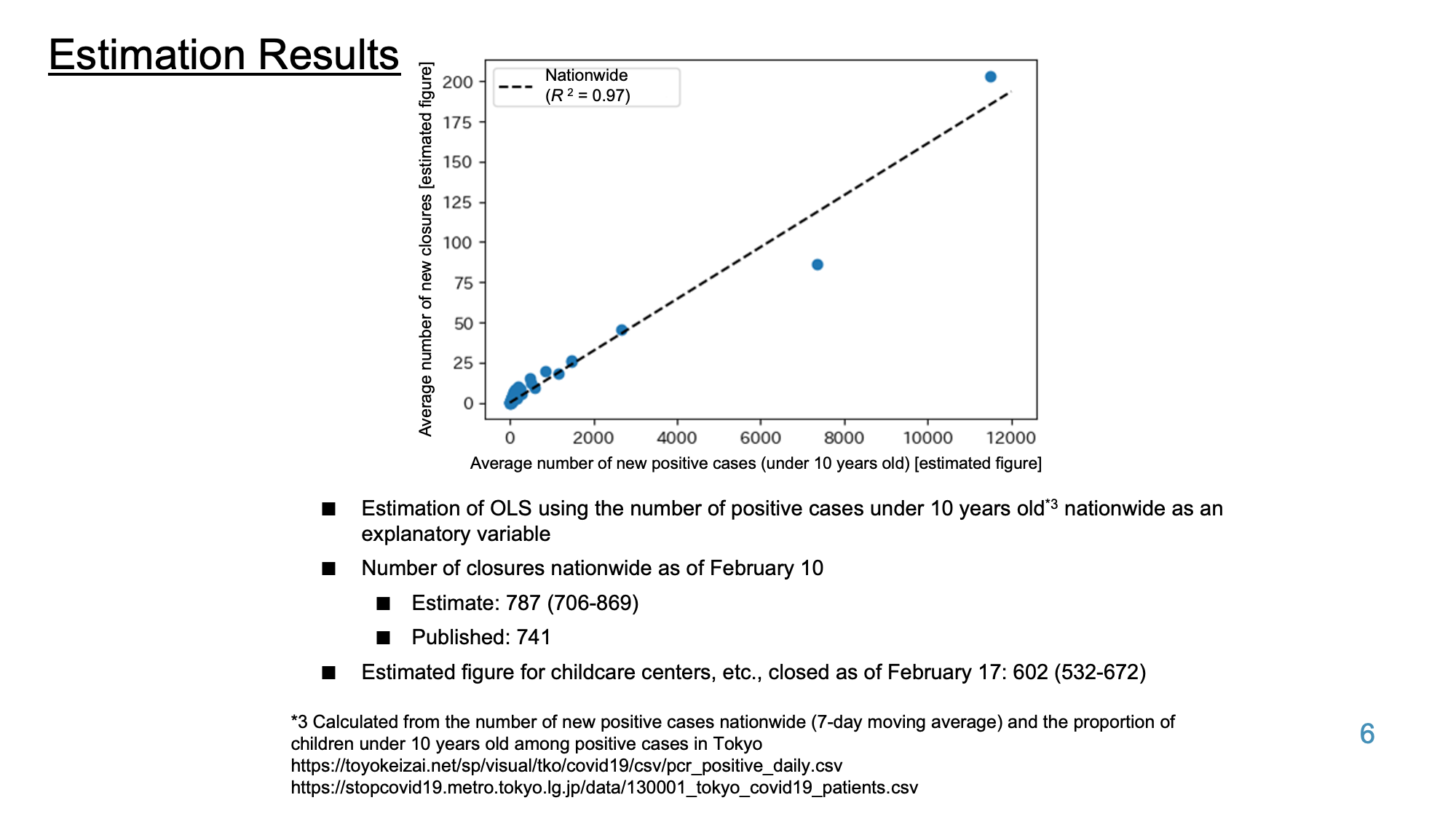
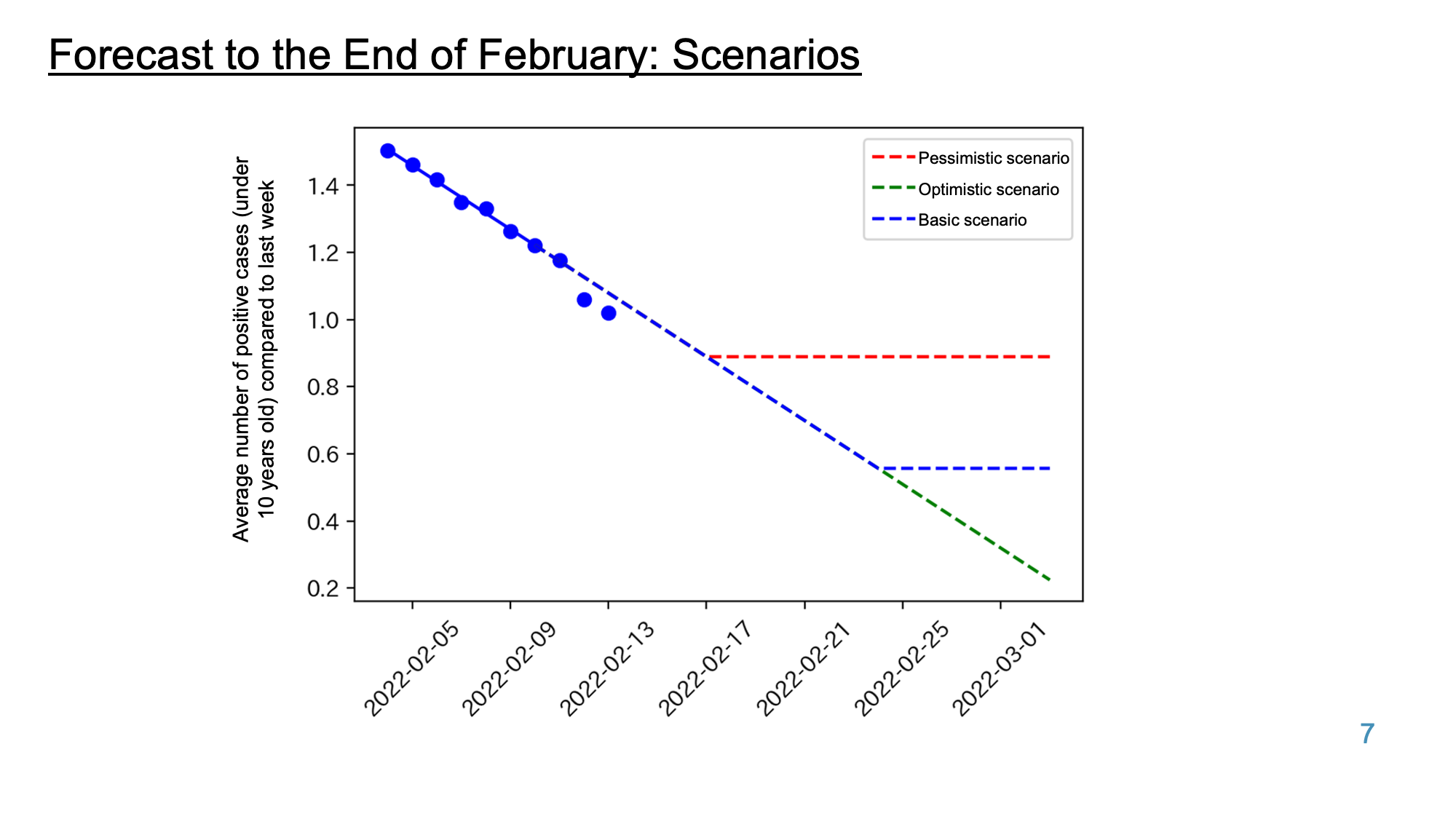
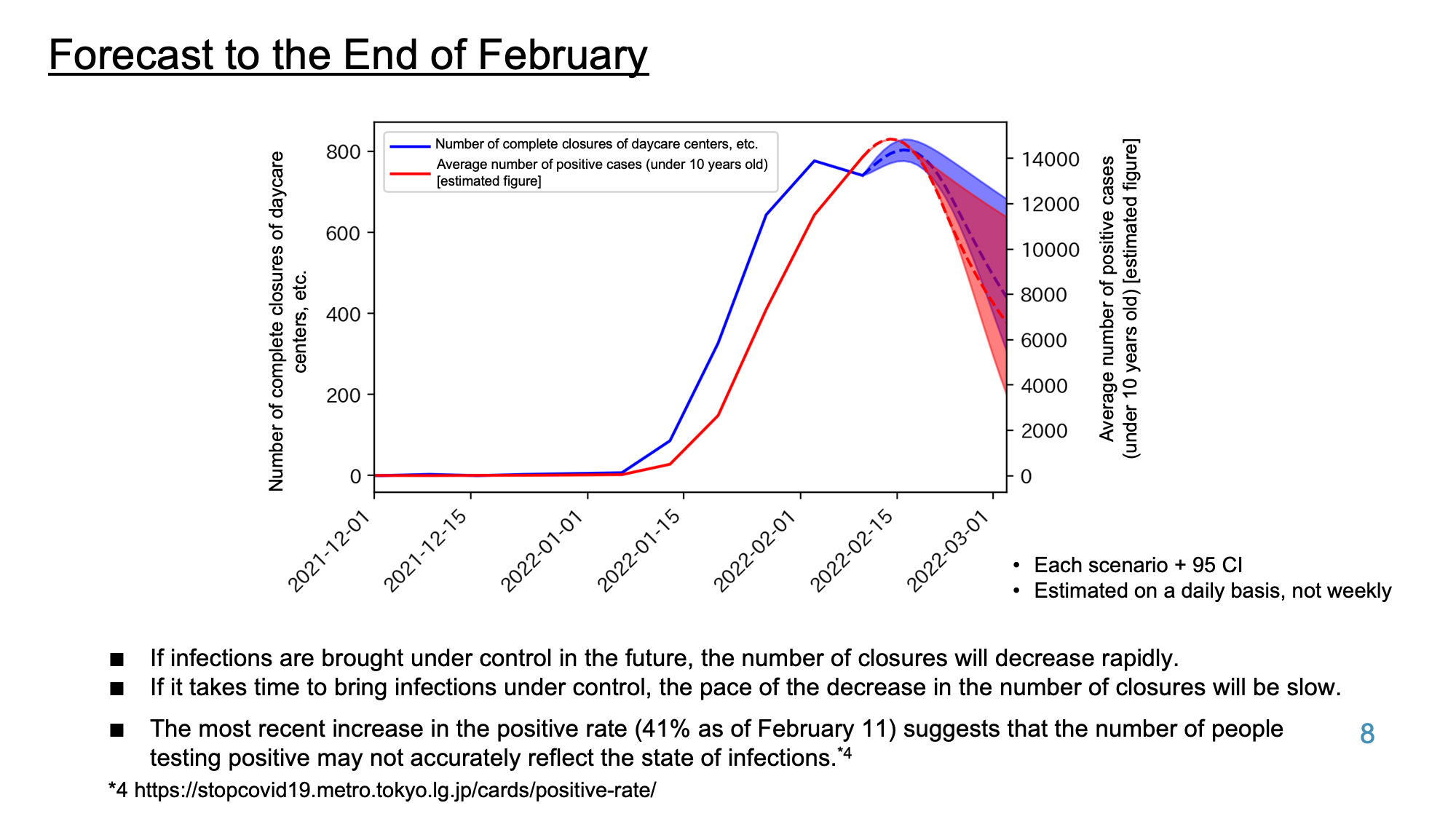
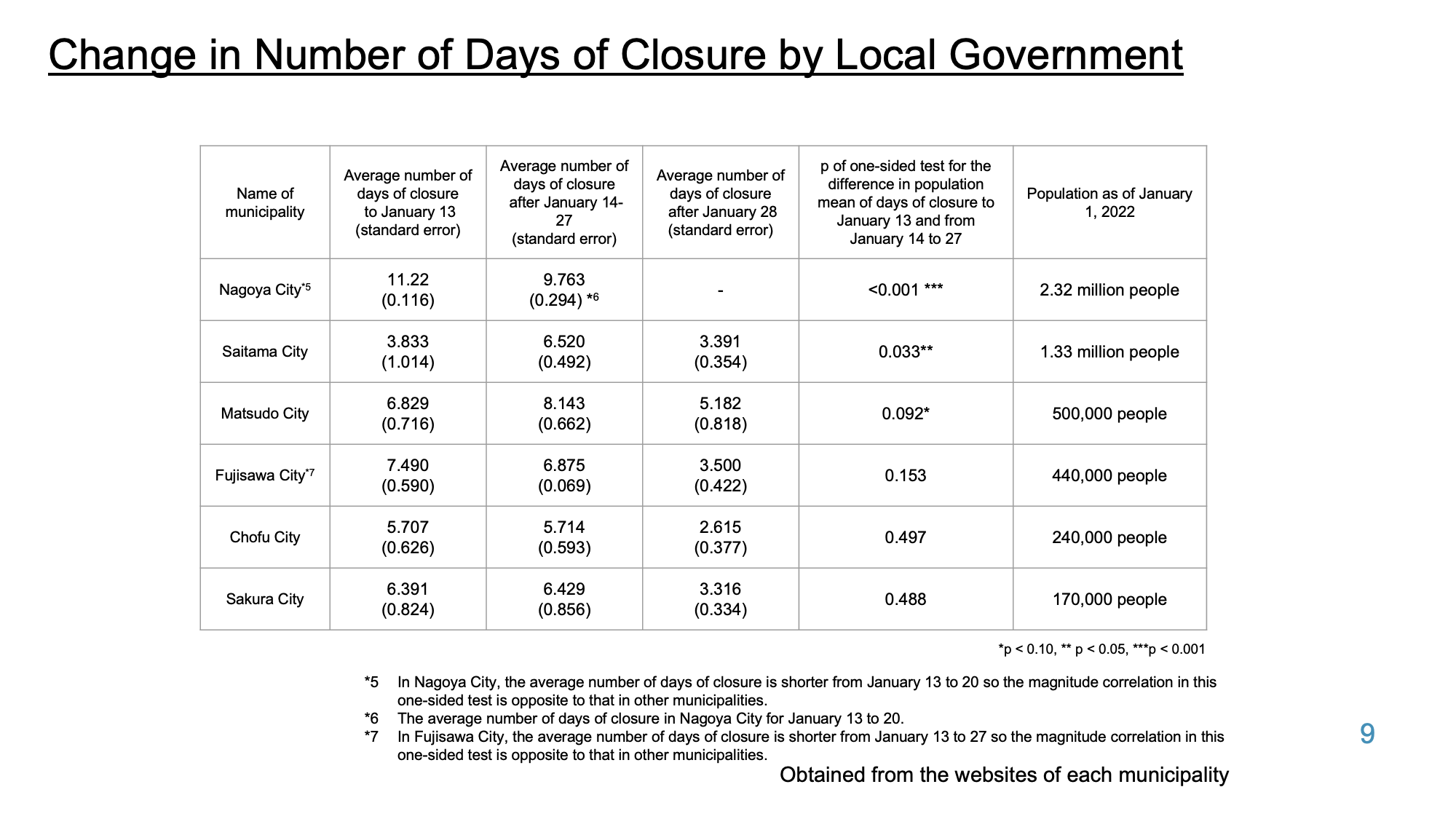
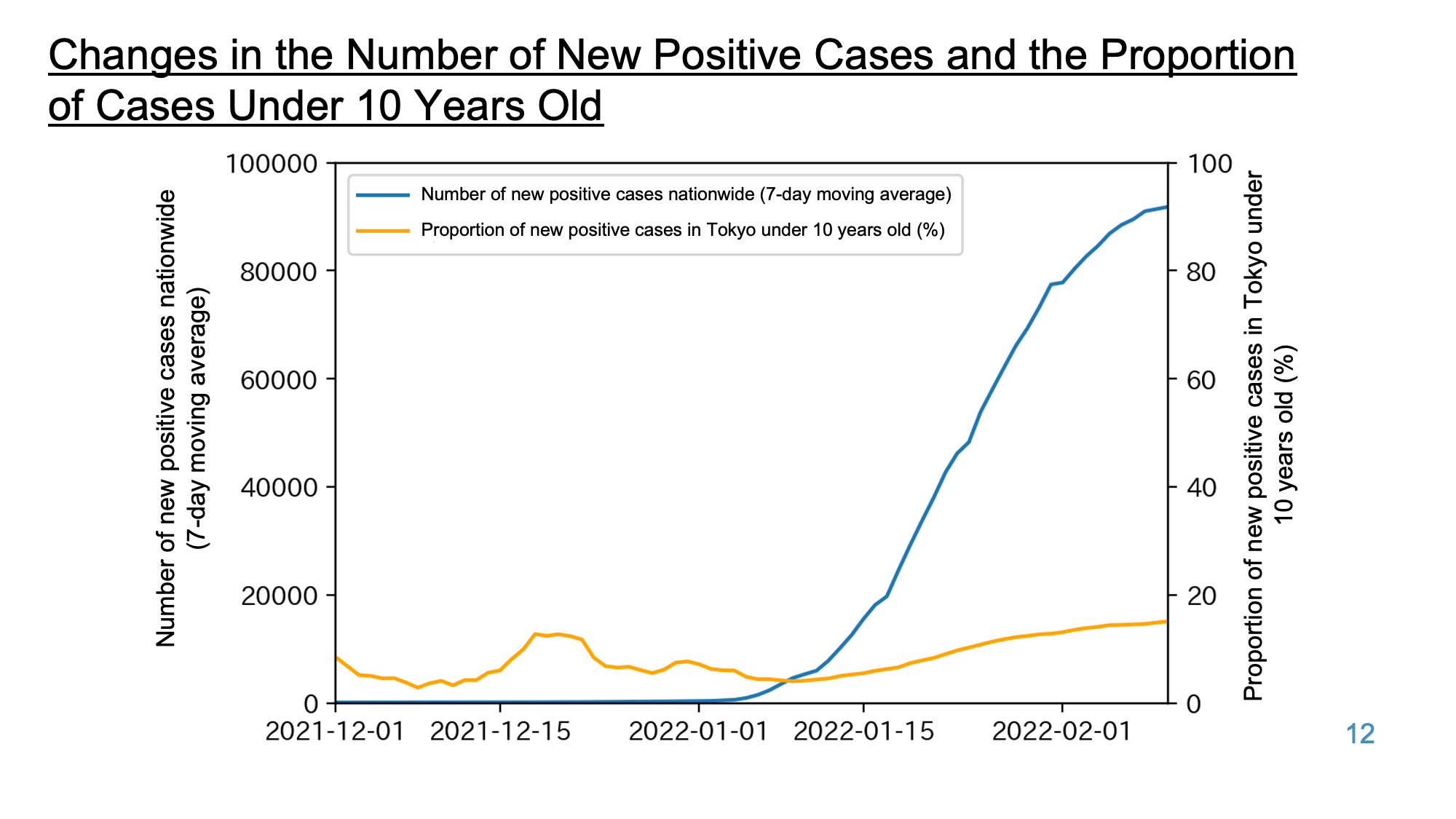
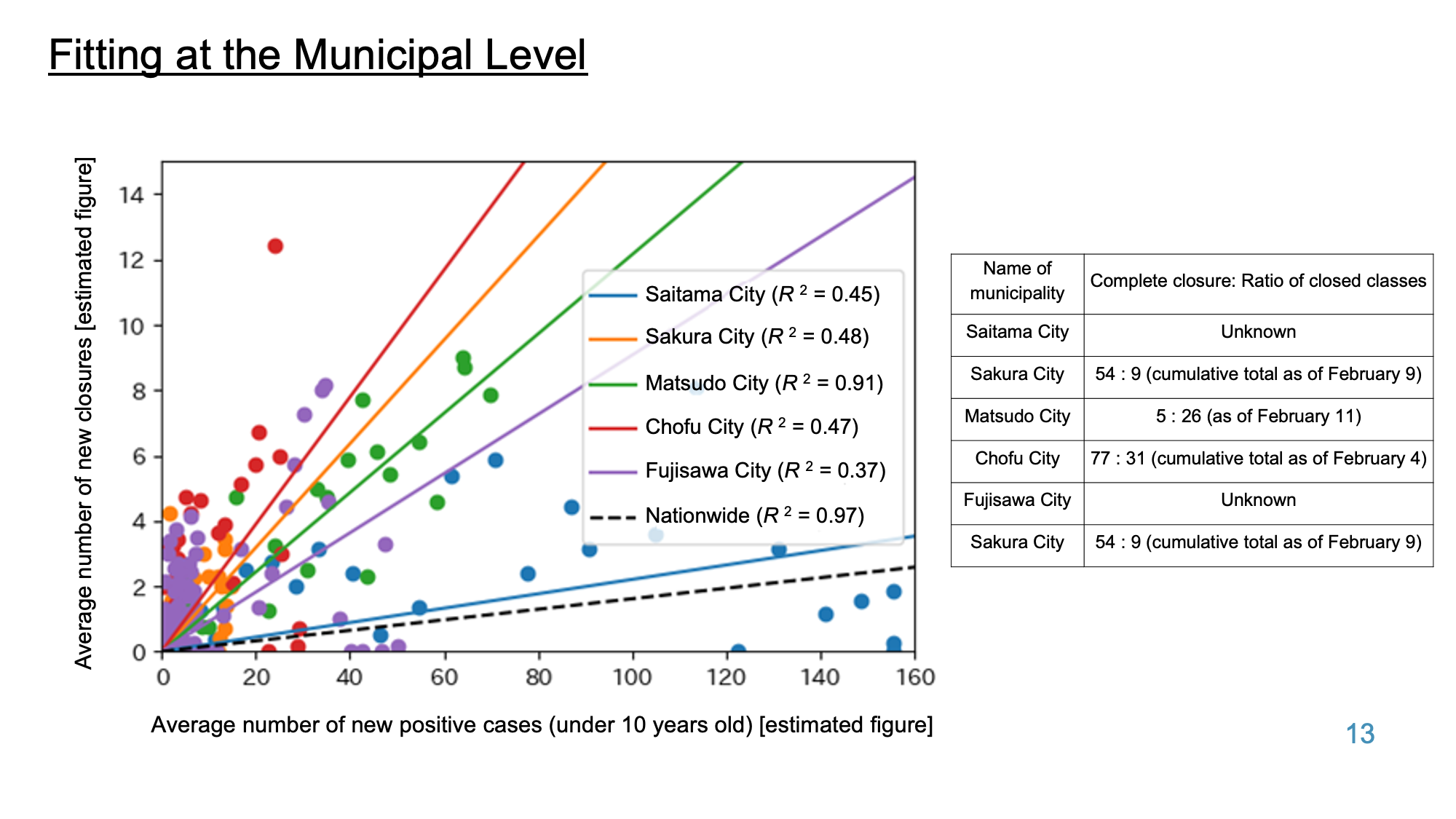
Estimates of the number of daycare closures

2022.02.15

Organization

The Tokyo Foundation for Policy Research

Researcher

Asako Chiba
/

Related reports

Estimates of new positive patients for Omicron variant (Tokyo) #7

2022.03.22

Organization

Graduate School of Business Sciences, University of Tsukuba

Researcher

Setsuya Kurahashi

Updates on prediction of new infections, severe cases, etc. #5

2022.03.22

Organization

Center of Biomedical Physics and Information Technology

Researcher

Akimasa Hirata

Outlook for COVID-19 and Economic Activity after the Lifting of Priority Measures to Prevent the COVID-19 Spread

2022.03.22

Organization

Graduate School of Economics, Faculty of Economics, The University of Tokyo

Researcher

Taisuke Nakata